What is a Greedy algorithm and why it is called greedy?
As the name suggests, Greedy tells the Greedy algorithm works or takes the step or should say
the best step (choice) present at that moment which will give us the optimal solution. It is mainly used in optimisation problems i.e. maximising or minimising something.
But that solution may be optimal or not. Isn’t it confusing? Actually no this algorithm takes the best option or way available at that moment without knowing the result of that path. So basically it means it is optimal for the current situation which may or may not result in optimal solution but always gives a feasible solution.
The important thing to remember in this algorithm is there should be optimal substructure and it never goes back (reverse) so if the best solution for that problem was available on another path it won’t be able to go back and hence it will have to look for optimal or best solution available from current situation. It’s a little bit tricky but I guess this example will give a fair idea about this algorithm.
Let’s understand with very famous Coin change problem. Suppose, you go to stationery for buying book and book costs Rs.65 and you give shopkeeper Rs.100 note and ask for change i.e. Rs.35 then you suddenly remind of your mother who said to make a change in the biggest note so you could not lose money anywhere coming back to home. Now the interesting thing is what is the greediest way of doing it?
- You ask for the biggest note that is Rs. 20 which is less than Rs.35.
- You need Rs.15 more so you ask the shopkeeper to give him Rs.10 note.
- Finally asking him to give you Rs.5 note which equals to Rs.35 i.e. change.
So what we did here is we chose the best solution available.
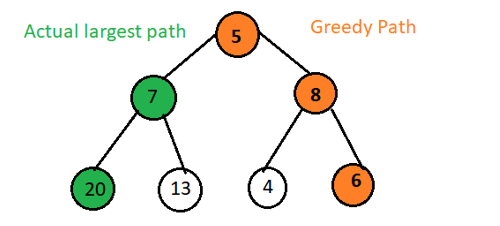
This image also gives a brief idea about this algorithm that at each node it takes the optimal step without knowing the result and value of each node at that path was greater when the step was taken. So this clearly shows the way it took was optimal for that situation but the overall result was not optimal.
Why use greedy if it’s not optimal in most of the cases?
Well in some cases greedy algorithm also gives a globally optimal solution rather
than giving locally optimal solution. Here are some of these algorithms:
- Prim’s algorithm (Minimum Spanning Tree)
- Kruskal’s algorithm (Minimum Spanning Tree)
- Dijkstra’s algorithm (Shortest Path)
- Huffman Coding (Data Compression)
Actually greedy problems are used in Graphs, Arrays, Some DP problems, NP-complete problems etc. Well, it’s not guaranteed it will give an optimal solution but when it will give that solution would be best.
Greedy Algorithms in Array:
There is no. of problems related to the greedy algorithm in an array. Let’s try to understand with a standard problem named
Activity Selection Problem: Problem Statement: You are given starting time and ending time of ‘n’ number of activities and you have to perform maximum activities in that time of span. Considering that you can only do one activity at a time.
e.g. starting_time = [10, 15, 20]
Ending_time = [20, 25,20]
You can perform a maximum two activities. The set of activities can be done is [0, 2] (indexes in starting_time and Ending_time). Here, the greedy choice will be if to do that activity whose finishing time is least then the remaining activities and starting time is more than or equal to ending time of the last activity.
- The first step is to sort the array according to their ending time
- Select the first element of sorted array and display it
- Perform following step for rest of the elements present in the sorted array
- If the starting time of this element is greater or equal to the last the selected element then select this element and print it.
C++ Solution: The complexity of this solution would be O(n) if the elements in an array are in sorted order and O (nlogn) if the array is unsorted.


Minimum absolute difference in array-
Problem statement: You are given an array of ‘n’ elements in it and you have to find the minimum absolute difference between any two elements in the array.
E.g. Suppose size of an array is 5 and arr [ ] = [ 2, 9, 0, 4, 5]
The output is 1 as 4 and 5 give the absolute difference of 1. Here, the important thing to note is you can also solve it by checking the difference of the first element with rest of elements then the Second element with rest of elements and so on which will bring this solution to the complexity of O(n2) which will not be a greedy approach. The greedy approach here will be if we sort the array and then see the difference.
Let’s see how:
After sorting the array it becomes arr [ ] = [0, 2, 4, 5, 9] and here as you can see that after sorting the array the difference between the first element and second element will be less than the rest of the elements and so on that’s why we don’t need to check one element with every other element which is the key here and it will bring the complexity of this solution to O(nlogn).
C++ Solution:

Weighted job scheduling-
Problem statement: You are given n jobs where every job is represented as:
- Start time
- Finish time
- Profit Associated
Find the maximum profit subset of jobs such that no two jobs in subset overlap. e.g. Let no. of job n=4
Job details {Starting_time, finishing_time, Profit}
Job 1: {3, 10, 20}
Job 2: {1, 2, 50}
Job 3: {6, 19, 100}
Job 4: {2, 100, 200}
Then we will get maximum profit of 250 with choosing job 2 and job 4
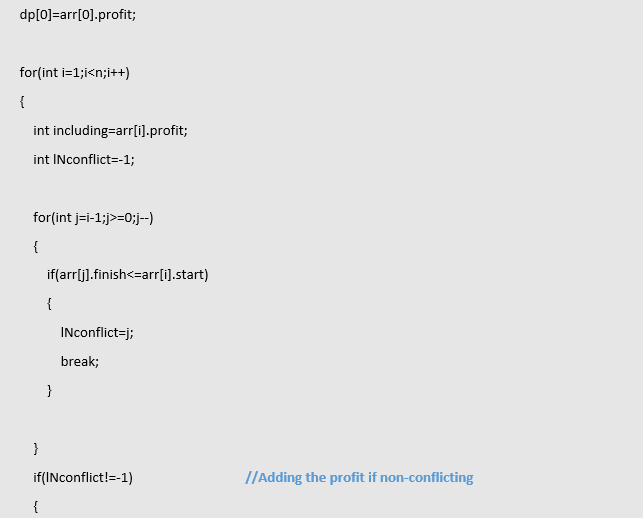
The first thing to do here is to see if jobs are conflicting but first sort the array on the basis of finishing time and can see which latest non-conflicting job you could have done before in the array. Now there could be two more cases including the current job or excluding so what does it mean? It means you don’t include the current job then the answer could be last latest job you could have done and If you’re doing the current job then you must do this. Suppose you have an array sorted on the basis of finishing time.
Here you will have to iterate through a loop from j=i-1 to j>=0 and see if(arr [j].finish <= arr[i].start) then include in profit.
One thing to note here is it is a combined problem of DP (Dynamic Programming) and Greedy algorithm. Then after storing in another array maximum from both including the current job and excluding it.
C++ Solution:



Although there is no. of problems for Greedy algorithm in Array few of them are:-
- Maximum and minimum product subset of an array
- Maximise and minimise array sum after k-negotiations
- Minimum increment/decrement to make array non-increasing
- Sorting array with reverse around the middle
- The minimum sum of the product of two arrays
- Sun of Areas of Rectangles possible for an array
- Find if k bookings possible with given arrival and departures time
- Minimum sum by choosing a minimum of pairs from an array
- Minimise the sum of the product of two arrays with permutation allowed
- Maximise height pyramid from the given array of objects
- Partition into two subarrays of lengths k and (N – k) such that the difference of sums is maximum
- Minimum operations to make GCD of array a multiple of k
Must do Greedy problems for placement/Interview Purpose:-
- Activity Selection Problem
- Kruskal’s Minimum Spanning Tree Algorithm
- Dail’s Algorithm
- Fractional Knapsack Problem
- Graph colouring
- Connect n ropes with minimum cost
- Boruvka’s Algorithm
- Dijkstra’s Shortest Path Algorithm
- Prim’s MST for Adjacency List Representation
- Minimise Cash Flow among a given set of friends who have borrowed money from each other
- Find maximum sum possible equal to the sum of three stacks
- Find minimum time to finish all jobs with given constraints
- Greedy Algorithm to find the Minimum number of Coins
- K Centers Problem
- Dijkstra’s Algorithm for Adjacency List Representation
- Efficient Huffman Coding for Sorted Input
- Prim’s Minimum Spanning Tree Algorithm
- Job Sequencing Problem
- Minimum Number of Platforms Required for a Railway/Bus Station
- Huffman Coding
Want to read more about algorithms? Click here.
By Yogesh Kumar














The best blog written. It actually gives a clear idea along with ample amount of examples
You are unbelievable man ❤💞❤
Good article on greedy algorithm….